你的鞋都比你聪明

这篇文章来自阮一峰的博客，讲了他关于未来智能的看法。

我概括下，我的观点。

1、从整体来看，人类的智能是有限的。

很多事物从统计学来看，不仅是人类智能还是知识还是职业发展，都跟正态分布离不开关系，

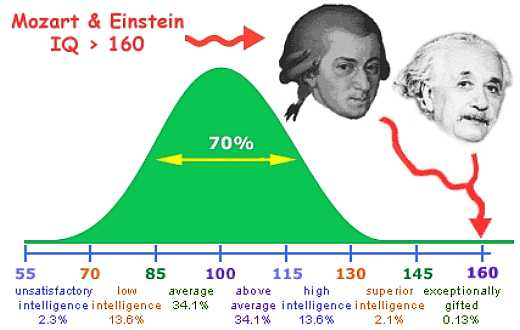
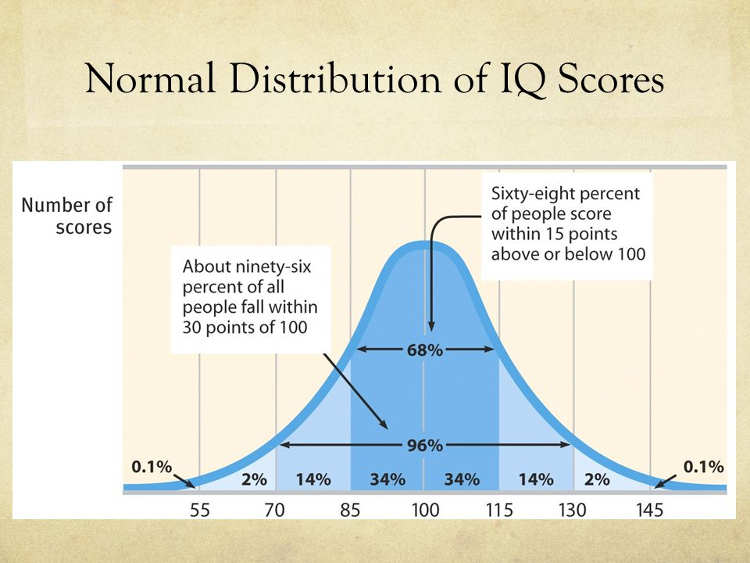
人类的智能是一个正态分布，IQ 测试假设平均智能是100，标准差是15，

继续阅读全文 »

twelfth-day

第十二天

我发现总结给予的效果不大，特别是在现在学的非常少的情况下。现在学的的知识看起来也是某种程度上的基础。可以被推导的事情，就不用记载了。

所以决定先静修一会，晚点再保持写总结[学科]笔记。

确保每次发布在网上的都会是能够帮助其他人学习的文章

继续阅读全文 »

英语笔记-2

包括以下词汇

  1. Linguistics - 语言学
  2. Prelude - 前奏
  3. Composite function - 复合函数

Linguistics [noun]

Meanings: The study of language in general and of particular languages, their structure, grammar, and history

记忆方法: Lin-guis-tic, 根据读音

e.g: Out with every theory of human behavior, from linguistics to sociology.

Linguistics 有很多的变形如：

去掉s【形容词】语言学的 - Linguistic [adjective]. e.g: She is pursuing her linguistic researches.

添加ian【名词】语言学家 - Linguistic-ian [noun]. e.g: The linguistician tolds us the rules of English grammar will help us a lot when writing some thesis and communicate with each other.

继续阅读全文 »

数学笔记-2

指数方程、微积分的预修条件

<!— more —>

先看一个有意思的指数方程问题

$\frac{m^\frac{7}{9}}{m^\frac{1}{3}} = m^\frac{k}{9}$ For m > 0

解法是根据指数的性质如：

$\frac{x^a}{x^b} = x^{1 - 2}$

$\frac{x^a}{x^b}=x^a\times \frac{1}{x^b} = x^a \times x^{-b}$

就意味着：

$m^{\frac{7}{9}-\frac{3}{9}}=m^\frac{k}{9}$

$\frac{k}{9}=\frac{4}{9} \Rightarrow k = 4$

o了。

简化多重根号问题：

$(r^\frac{2}{3} s^3)^2{\sqrt{20r^4s^5}}$

$\Rightarrow (r^\frac{2}{3})^2 \cdot (s^3)^2 \cdot (4\cdot 5 \cdot r^4 \cdot s^4 \cdot s)^\frac12$

$ \Rightarrow r^\frac{4}{3} \cdot s^6 \cdot 4^\frac{1}{2} \cdot 5^\frac{1}{2} \cdot r^2 \cdot s^2 \cdot s^\frac12$

$\Rightarrow r^\frac43 \cdot r^2 \cdot s^6 \cdot s^2 \cdot s^\frac12 \cdot 4^\frac12 \cdot 5^\frac12$

$\Rightarrow r^{3\frac13} \cdot s^{8.5} \cdot 2 \cdot \sqrt5$

简化的方式有很多，选择任意一样你想要或喜欢的。

O了！

负数是可以求奇数根的。如 $\root{3}\of{-27} = -3$

偶数根则不行

在明白了这些性质和概念之后，我们可以直接进一步学习下一课程了。

刷了下题后，通过了有理指数-求根单元测试

于是便来到了函数

函数第六单元前都是些简单的介绍和加减乘除之类的

函数的组合，从加减乘除函数开始，这些都比较简单。

到了复合函数如:

$f(g(o))$

$\ g(f(o))$

其实跟编程里的函数没差啦，理解起来还是挺轻松的。

1
Math.sqrt(Math.abs(-4)) === 2  // outputs true

如何根据图表📈分析是否是函数

这是光头做的讲解。光头说函数只取一个值然后仅仅输出一个值，这就意味着$x$映射着输出$y$，如果多出来一些奇怪的值，那这肯定不是一个函数。在函数式编程中这被称为带有副作用的函数。

如：

就是有效函数。

而

就不是一个有效的函数。

eleventh-day

第十一天的总结

以后笔记会用来做总结今天学习和发生了什么, 其它学科总结将移步到相应的[学科]笔记

今天的所学的知识包括

数学

  1. 有理指数和求根 - Rational exponents & radical
  2. 函数

英语

  1. Linguistics
  2. Prelude

Wolfram 的 Mathematica系统

  1. Mathematica简称mma，是一款在数学界挺热门的一款编程系统，它可以写各种公式，画图。还有自然语言处理和使用机器学习的能力。真的是太Amazing了。
  2. 不仅如此，mma还被应用于物理，生物信息学，地理，语言学，网络分析，光学，风险管理，软件工程等等等等等。
  3. 介绍俩本关于mma编程的书籍📚

继续阅读全文 »

英语笔记-1

词汇：

interpretation [noun]:

1. the way in which someone explains or understands an event, information, someone’s actions etc. (人们解释或理解某些事情的方式，信息，人们的行动等等)
e.g: One possible interpretation is that they want you to resign.
e.g: It’s difficult tot put an accurate interpretation on (= explain) the survey results.
e.g: Is there only one interpretation?

2. the way in which someone performs a play, a piece of music etc and shows what they think and feel about it (大致就是说可以用于关于音乐和演出的演绎、处理方式)
e.g: Laurence Olivier’s brilliant interpretation of Henry V

tenth-day

第十天

​ 做下关于这十天的总结。

这十天中学习的差不多都是初中知识。看的都是英语材料（因为可以顺便锻炼英语），现在发觉理论缺乏的太多了，虽然说速度已经够快了。但是这个速度还是不够。

说起来这十天为了安排住所跟网线和打狂犬疫苗的事情浪费了很多时间。

这里包括了我学习的网站，algebra 1的课程列表，所需要学的高中知识列表等

继续阅读全文 »